二叉树(第23节~29节)
非原创。本文来自王争老师在Geektime的《数据结构与算法之美》专栏。
二叉树的存储方式:
链式存储:
遍历方式:左右子节点
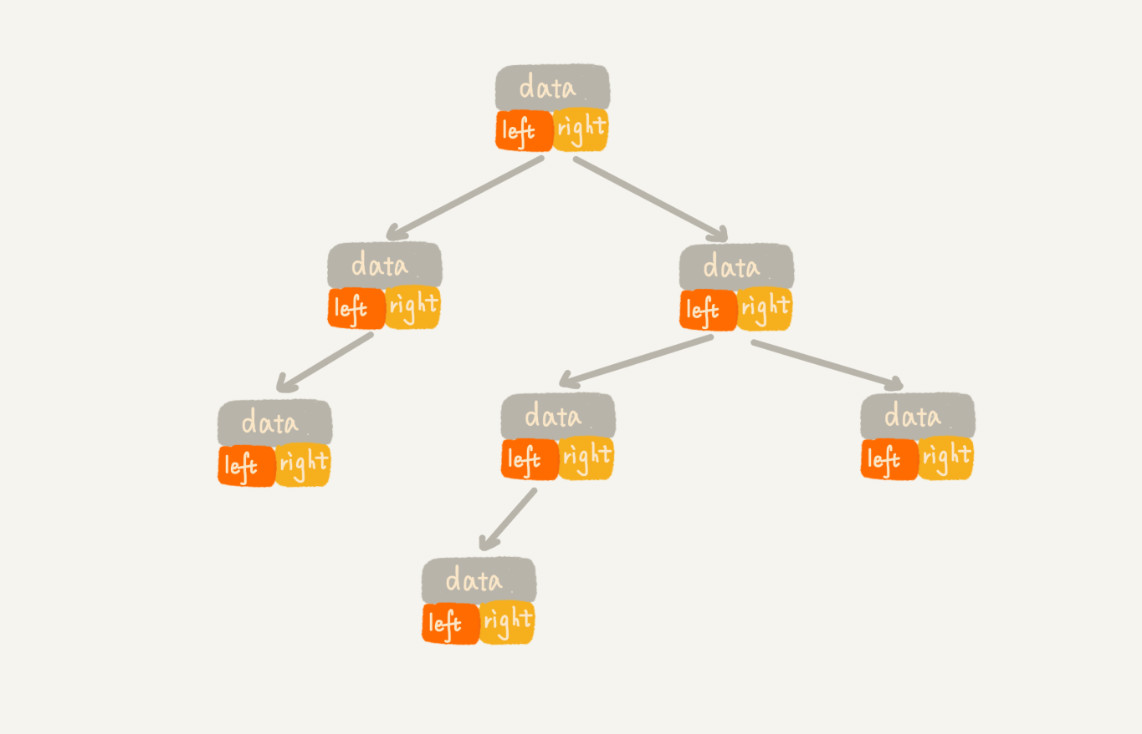
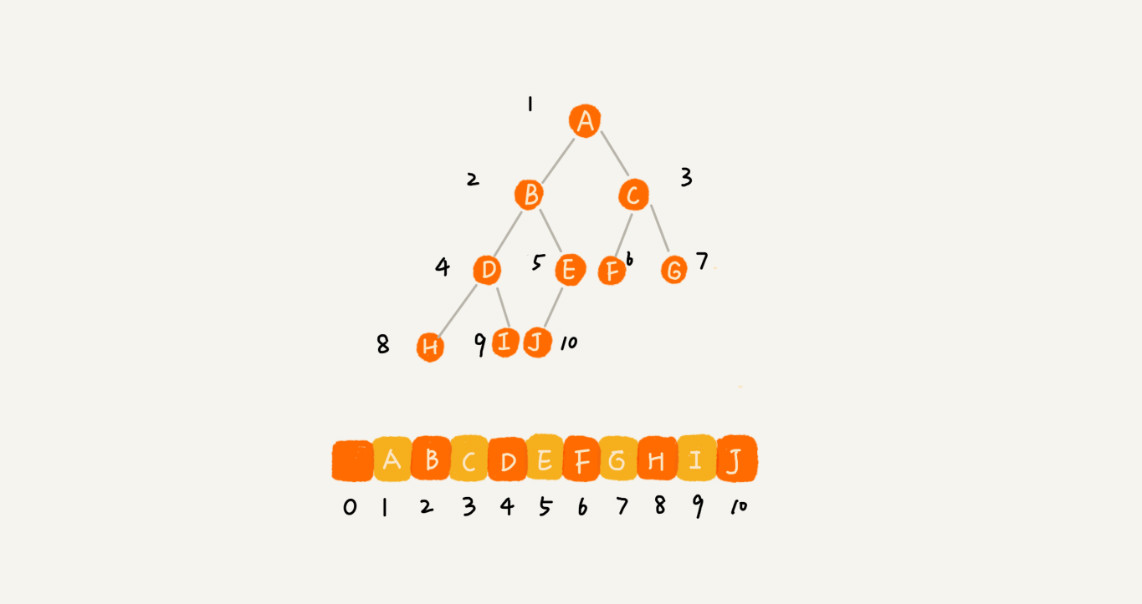
数组存储:
遍历方式:节点X存储在数组中的下标为i,那么它的左子节点的存储下标为2 i,右子节点的下标为2 i + 1,下标i / 2位置存储的就是该节点的父节点
数组顺序存储的方式比较适合完全二叉树,其他类型的二叉树用数组存储会比较浪费存储空间
二叉查找树
定义:
二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值
插入操作:
若要插入的数据比该节点的数据大,与右子树比较;若比该节点小,与左子树比较,知道遍历到null,插入节点
删除操作:
- 若要删除的节点只有一个字节点,将该节点替换为其子节点
- 若有两个子节点,将该节点替换为左子树中最大或者右子树中最小
重复数据操作:
- 类似于Hash表的拉链法
- 把新插入的值当作大于这个节点的值来做插入操作
AVL树
自平衡二叉查找树
平衡因子: 某个结点的左子树的高度减去右子树的高度得到的差值
AVL 树: 所有结点的平衡因子的绝对值都不超过 1 的二叉树。每次插入和删除操作都会更新沿途节点的高度值和平衡因子。通过旋转来平衡化
旋转
左旋转、右旋转这两种操作都是从失去平衡的最小子树根结点开始的(即离插入结点最近且平衡因子超过1的祖结点)。并且以子树为原点的:如b是a的子树,那么旋转就围绕b来进行
旋转实现:
AVL树的旋转图解和简单实现
缺点:插入、删除破坏平衡时,需要平衡化,比较耗时,代价较高
红黑树
一种近似平衡的二叉查找树,它能够确保任何一个节点的左右子树的高度差不会超过二者中较低那个的一倍
规则:
- 每个节点要么是红色,要么是黑色
- 根节点必须是黑色
- 红色节点不能连续(也即是,红色节点的孩子和父亲都不能是红色)
- 对于每个节点,从该点至null(树尾端)的任何路径,都含有相同个数的黑色节点
put操作:插入节点必须是红色,新插入的节点都放在叶子节点上
破坏红黑树规则的情况:
当前节点的父节点是红色,且当前节点的祖父节点的另一个子节点(叔叔节点)也是红色
(1) 将“父节点”设为黑色
(2) 将“叔叔节点”设为黑色
(3) 将“祖父节点”设为“红色”
(4) 将“祖父节点”设为“当前节点”(红色节点);即,之后继续对“当前节点”进行操作。
当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的右孩子
(1) 将“父节点”作为“新的当前节点”
(2) 以“新的当前节点”为支点进行左旋
当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的左孩子
(1) 将“父节点”设为“黑色”
(2) 将“祖父节点”设为“红色”
(3) 以“祖父节点”为支点进行右旋
remove操作:
删除点p的左右子树都为空,或者只有一棵子树非空
(1)将p删除(左右子树都为空时),或者用非空子树替代p(只有一棵子树非空时)
(2)若破坏了红黑树规则,按照put节点时的思路添加
删除点p的左右子树都非空
(1)用p的后继s(树中大于x的最小的那个元素)代替p,然后使用情况1删除s
p节点的后继结点:
- p结点的右子树不空,则p的后继是其右子树中最小的元素
- p结点的右子树为空,则p的后继是其左子树中最大的元素
递归树求算法时间复杂度
实战一:快速排序
假设每次分区的比例为1:k。k=9时。
递归分解过程:
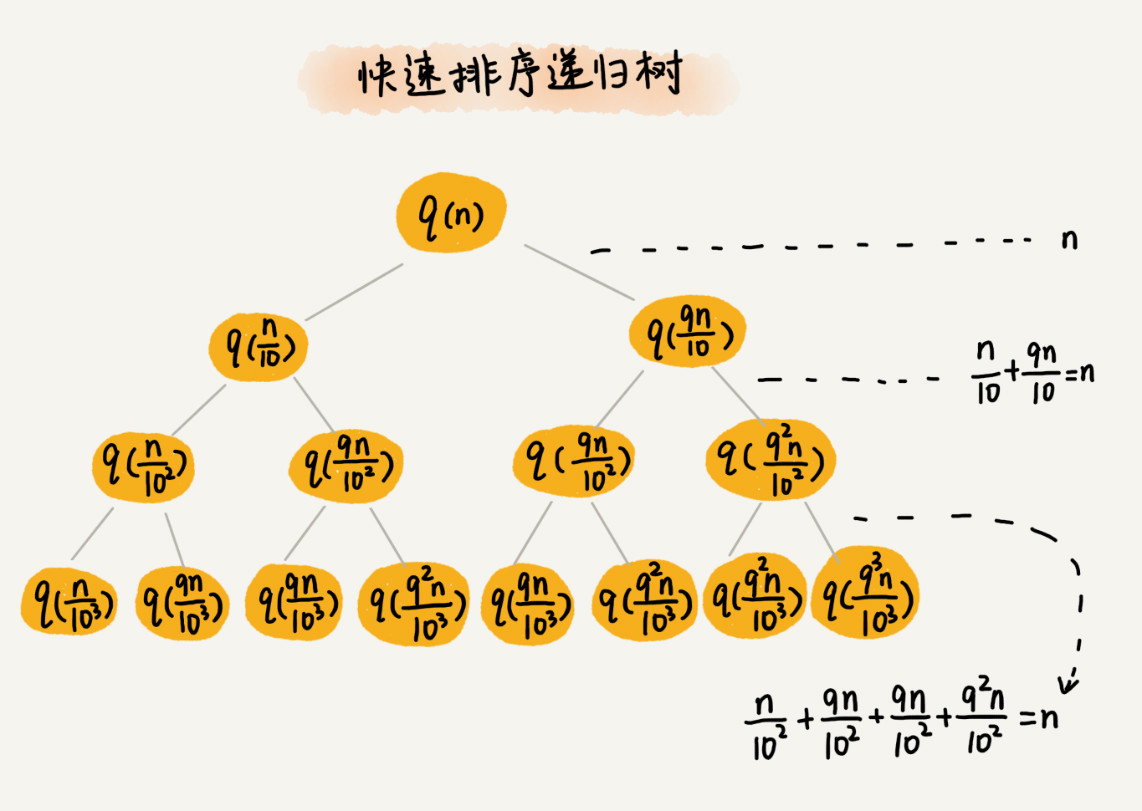
每层遍历数据个数为n,需要求出遍历层数h,即递归树高度h,即可算出快排时间复杂度为O(h*n)
高度h的计算:
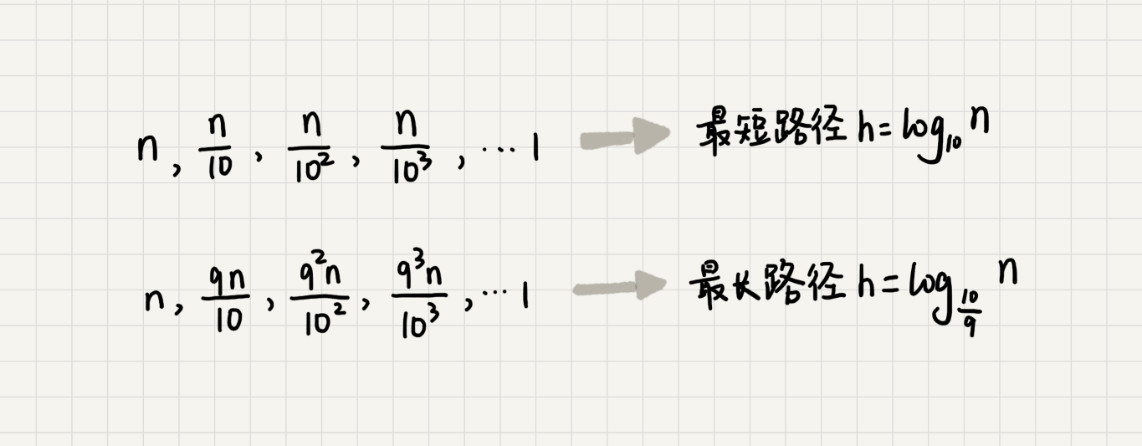
快排的时间复杂度为:O(nlogn)
堆和堆排序
堆
堆的条件:
- 堆是一个完全二叉树
- 堆中每一个节点的值必须大于等于(或小于等于)其子树中每个节点的值
增加数据:
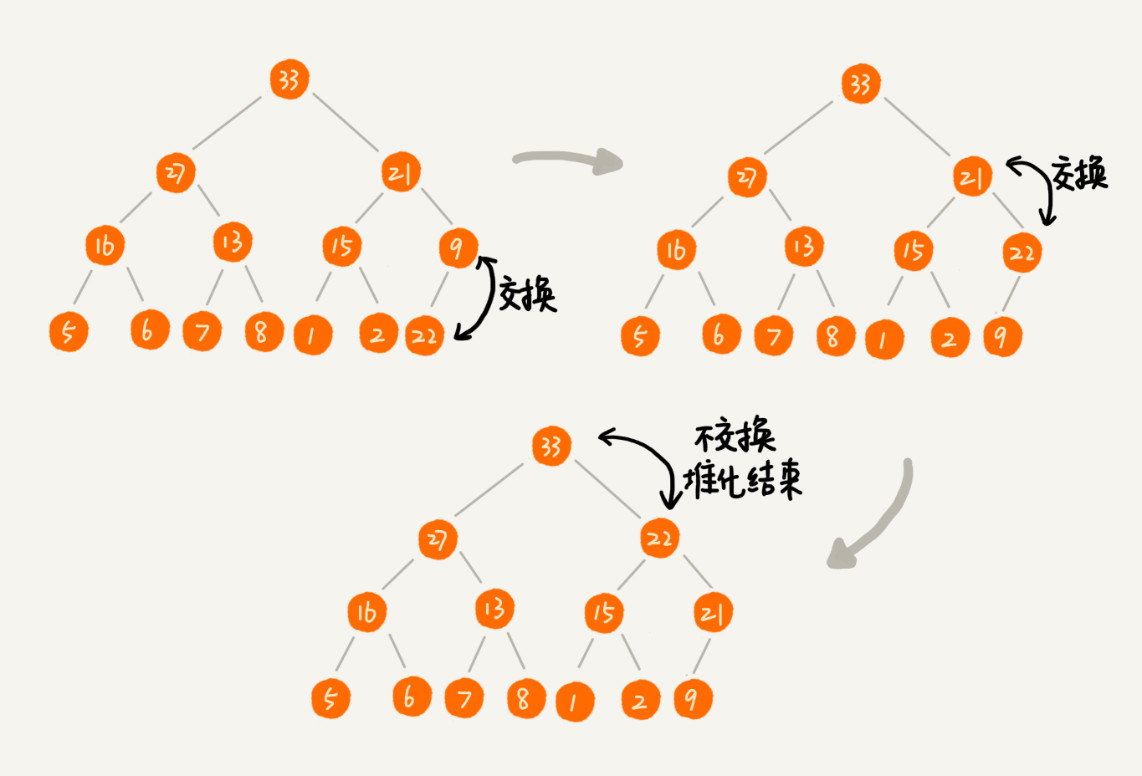
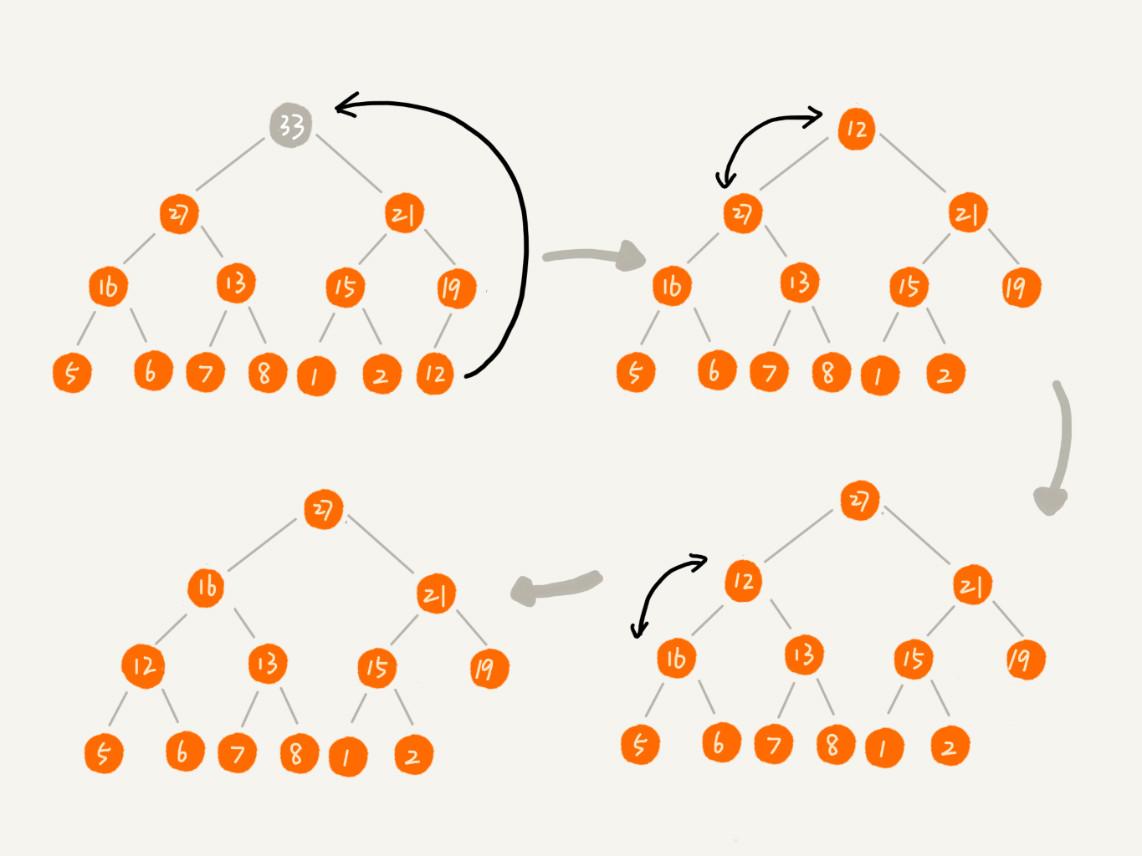
删除堆顶数据:
堆排序两步:
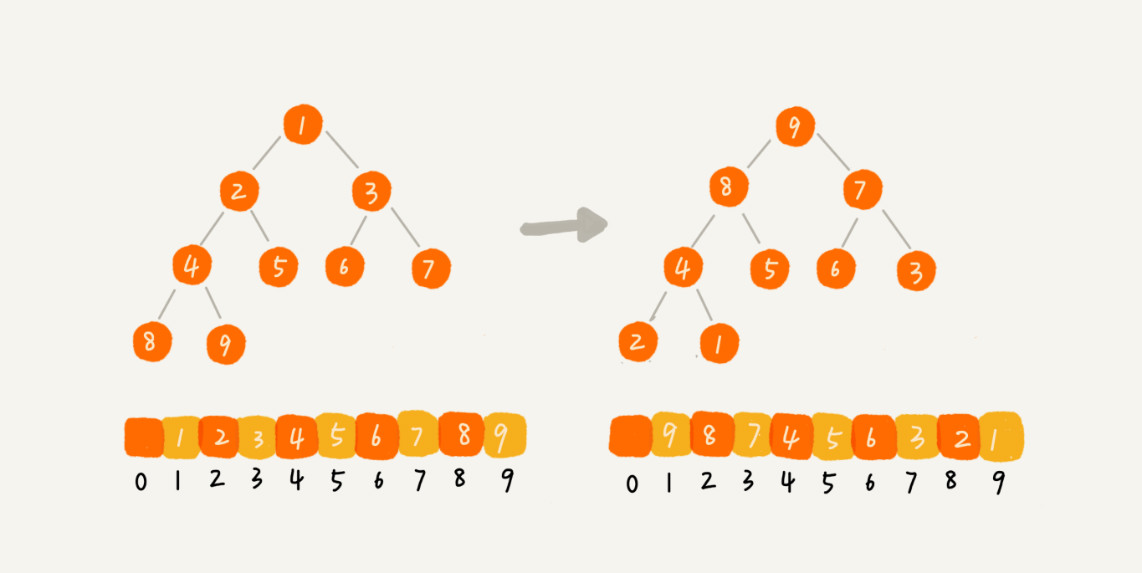
一、建堆 时间复杂度O(n)
- 思路一:在堆中插入一个元素的思路。尽管数组中包含n个数据,可以假设起初堆中只包含一个数据,即下标 为1的数据。
- 思路二:从堆中的第一个非叶子结点向根节点,依次堆化。
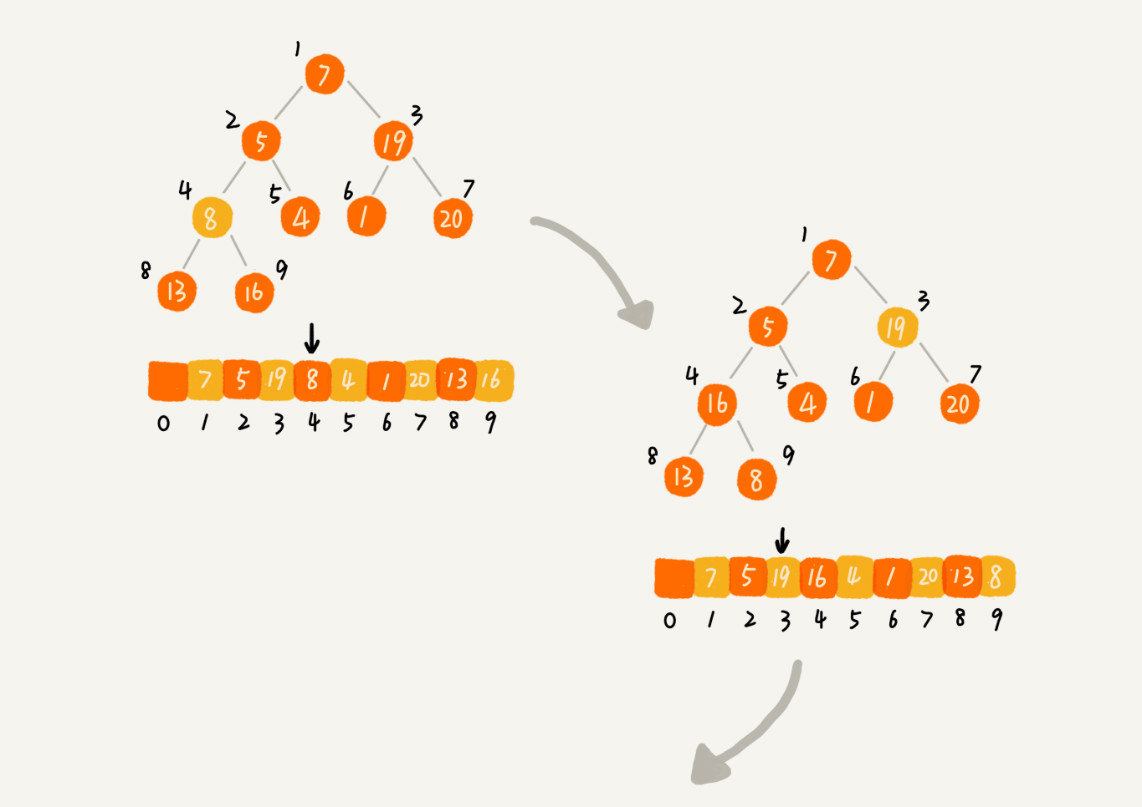
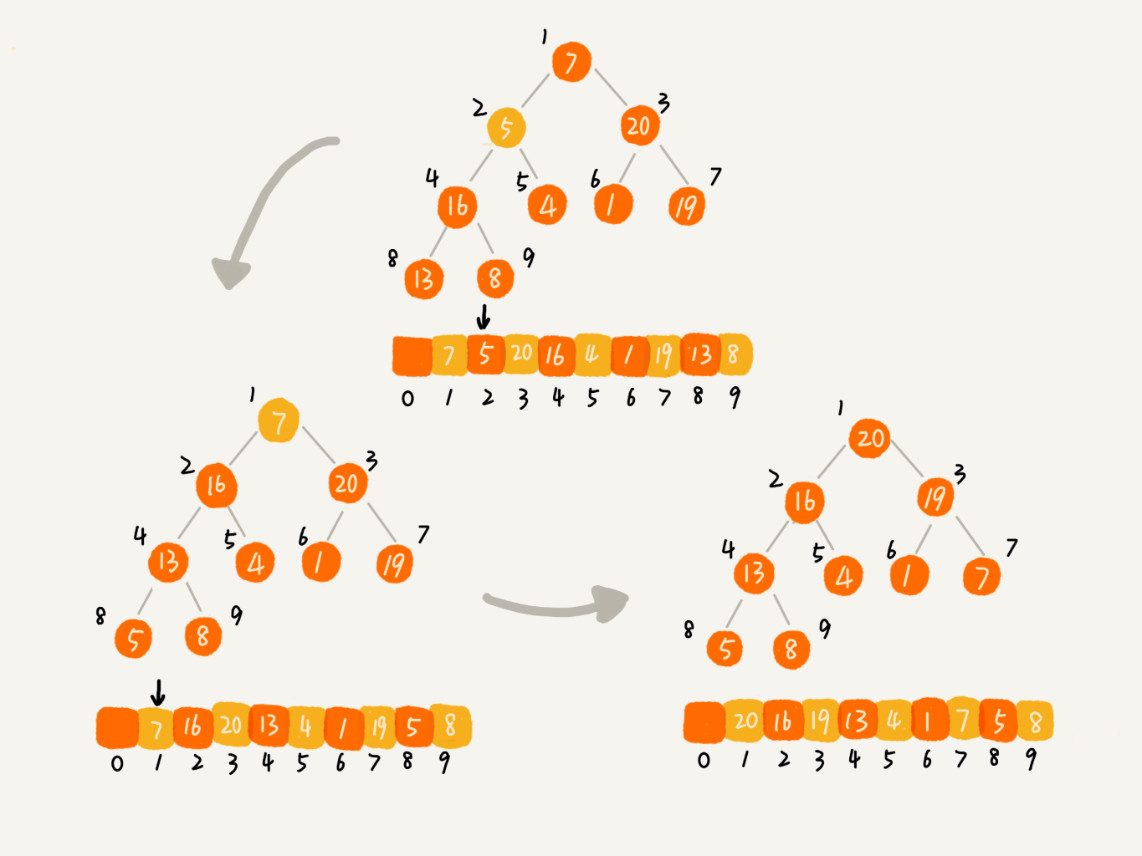
二、排序 时间复杂度O(nlogn)
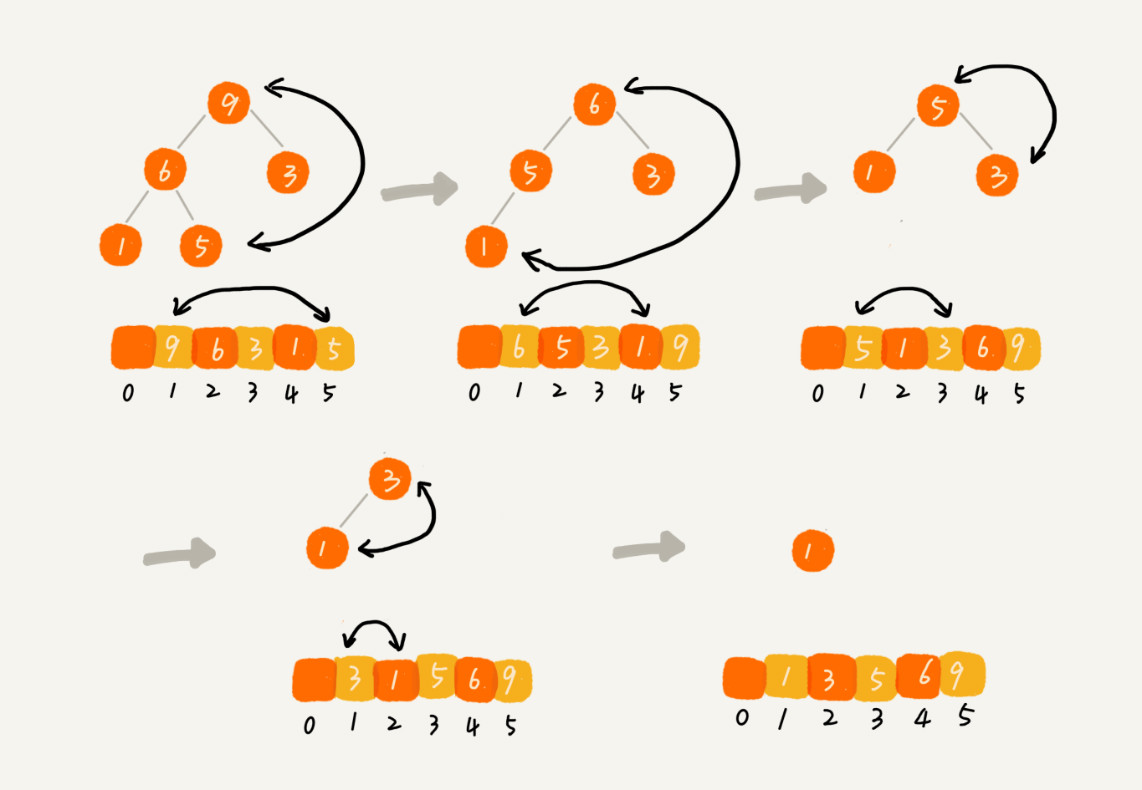
空间复杂度:O(1) 时间复杂度:O(nlogn) 不稳定
为什么快排比堆排序性能好?
数据访问方式。快排是顺序访问,堆排是跳着访问。实质是与缓存淘汰/页面置换有关。
堆排数据交换次数较多。堆排可以看成是高级排序中的冒泡排序,太多无用功的数据交换。即建堆时会打乱数据原来的有序度。
堆的应用
一、优先级队列
堆顶元素优先级最高(或最低)
合并有序小文件:假设我们有 100 个小文件,每个文件的大小是 100MB,每个文件中存储的都是有序的字符串。我们希望将这些 100 个小文件合并成一个有序的大文件。这里就会用到优先级队列。维护一个size为100的小根堆。
定时任务队列:通过维护一个按剩余时间排序的小根堆。
(问题:如果父子节点剩余时间相差不大,进行堆化时效率很低,所以我认为,堆并不适用于定时任务队列。定时任务:Redis的过期字典、环形队列处理)
二、利用堆求Top K
维护一个size为K的小根堆,遍历数组与堆顶数据比较,并进行堆化操作。动态数据同理。
三、利用堆求动态数据集合的中位数
维护两个堆,一个大根堆,一个小根堆。大根堆中存储前半部分数据,小根堆中存储后半部分数据,且小顶堆中的数据都大于大根堆中的数据。
四、如何求接口的99%响应时间?
一个大根堆,一个小根堆。假设当前总数据的个数是 n,大根堆中保存 n 99% 个数据,小根堆中保存 n 1% 个数据。大根堆堆顶的数据就是我们要找的 99% 响应时间。
求Top K时,用堆排 or 快排?
堆排相比快排的缺点:
- 时间复杂度高,堆排O(nlogK),快排的优化O(n)(见第12节)
- 性能低,堆排的寻址效率低 & 交换次数高
- 原数据有序度越高,堆排效率越低
堆排相比快排的优点
- 空间复杂度低,堆排原地排序空间复杂度为O(1),快排空间复杂度为O(logn)~O(n),会有栈溢出的风险
- 对动态数据集的操作效率更高。
- 原数据有序度越低,堆排效率越高。
- 最坏情况下,堆排时间复杂度为O(nlogK),快排的时间复杂度为O(n*K)
总结:可以根据业务场景需要的特性而选择不同的排序算法。如果性能(综合时间复杂度、缓存性能等)差距不大,还是建议选择堆排。